�� �T���v��-1 �e�L�X�g����
1.4�́@�L���v�f�@�̊�b�T
��4-1 �L���v�f�@�̊T�v �A S *****
�i1�j�A�́u�v�f���v�ł͂Ȃ��A�u�ߓ_���v�ł���ׂ��Ȃ̂ŁA���炩�Ɍ��ł���B
�i2�j���͉���̒ʂ�B�I�����̕��͂͏��Ȃ��Ƃ��ËL���邱�ƁB
��4-2 ���U�� �B S *****
�i1�j�X�̎�@�̒��g��S���ËL����K�v�͂Ȃ��B�e��@���A���U����@�Ȃ̂��A
�A���ꎟ�������̉�@�Ȃ̂����ËL���邱�ƁB���A�D��S�ŁAWikipedia����
�ǂނ̂͗ǂ����Ƃł���B�܂Ƃ܂��������ǂނƋp���ĈËL���₷�����̂ł���B
�i2�j�B���������Ȃ��̂́A���炩�B
��4-3 �Ђ��݃G�l���M �C S ****
�i1�j����̎傽��̕��ł́A���Ԃ�������߂���B
�i2�j�Ђ��݃G�l���M=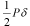 �͈ËL���邱�ƁB �͈ËL���邱�ƁB
�i3�j�ʉ��́A���Ԃ�������Ȃ��ėǂ��B������𗝉����āA�ËL���邱�ƁB
��4-4 �Ђ��݃G�l���M �A S *****
�i1�j�Ђ��݃G�l���M�̐ϕ����͈ËL���邱�ƁB����1/2�ɗ��ӂ��邱�ƁB
�i2�j�S�Ă̐������A�R��Ȃ��������킳��Ă��邱�ƁB
�i3�j����ćA���������B
��4-5 �Ђ��݃G�l���M �B F *****
�i1�j����̓�̐}���ËL����A���͎����ł���B
�i2�j�|�e���V�����G�l���M�A�R���v�������^���G�l���M�A�ǂ������`�����ËL���邱�ƁB
��4-6 ���U��-�G�l���M���� �B F *****
�i1�jΠ=ku2/2 - fu�͈ËL���邱�ƁB����fu�ɕ������t�����Ƃ��o���邱�ƁB
�i2�j�ŏ��|�e���V�����G�l���M�̌����́AδΠ=0�ł��邱�Ƃ��ËL���邱�ƁB
��4-7 ���U��-�G�l���M���� �@ S *****
�i1�j�ËL�̂݁B�A���A������̎��̈ËL�͕s�v�B
�i2�j���͖@�Ƃ����̂́A�u�ߓ_�̓����ߓ_�͂𖢒m���Ƃ���v�ł��邱�Ƃ��ËL���邱�ƁB
��4-8���z�d���̌��� �@ S *****
�i1�j�ꌩ������A�ӊO�ɊȒP�B
�i2�j���͂̂Ȃ����z�d��=�O�͂̂Ȃ����z�d���̕����o���₷���B
�O�͂̂Ȃ��d���ɁA����������̂��s���Ɨ��Ȃ��B
�i3�j�d��=�� x �ψ� �Ȃ̂ŁA�����͎����B�|�����킹��͂ƕψʂ͓������ނ̂��̂ł��邱�ƁB
�� �T���v��-2 �ËL���ڏW����
4��
�i1�j�L���v�f�@�̊T�v�i4-1�j
�ia�jFEM�ł́A���w�I�ɕΔ����������ŋL�q�ł���A���̖̂����������Ƃ��o����B
�ib�jFEM�ł́A�ߓ_���������ł���A��ނ̈قȂ�v�f��p���Ă�
�R���s���[�^�ɂ�����K�v�ȃ������e�ʂ͕ς��Ȃ��B
�ic�jFEM�ł́A �ΏۂƂȂ�̈���ŁA�x�z������������悤�ɋߎ������������B
�id�jFEM�ł́A�ϕ������ƃK���[�L���@���A���_�I��b�ƂȂ��Ă���B
�i2�j���U���i4-2�j
�ia�j�K���[�L���@�́A���U����@�B
�ib�j���C���[�E���b�c�@�́A���U����@�B
�ic�j�K�E�X�E�U�C�f���@�́A�A���ꎟ�������̉�@�B
�id�j�����@�́A���U����@�B
�i3�j�Ђ��݃G�l���M�i4-4�j
�ia�j 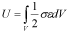
�ib�j���e���̏ꍇ�A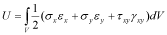
�i4�j���U��-�G�l���M�����i4-7�j
�ia�j���͖@�Ƃ����̂́A�u�ߓ_�̓����ߓ_�͂𖢒m���Ƃ���v�L���v�f�@�̈��
�莮���ł���B�w�ǂ̗L���v�f�@���p�R�[�h�́A�u�ߓ_�ψʂ𖢒m���Ƃ���v
�ψʖ@�̒莮�����̗p���Ă���B
�ib�j�ψʖ@�ł́A���z�d���̌������A���͖@�ł́A�≼�z�d���̌�����p����B
�i5�j���z�d���̌����i4-8�j
�ia�j���͂̂Ȃ����z�d��=�O�͂̂Ȃ����z�d��
�ib�j�d��=�� x �ψʁB�|�����킹��͂ƕψʂ͓������ނ̂��̂ł��邱�ƁB
�i6�j���z�d���̌����i4-9�j
�\�����̐����ł́A��肪����Ȓލ�����ԂɗL��A�|�e���V�����G�l���M��
�ŏ��ɂȂ��Ă���B
�i7�j���z�d���̌����i4-10�j
�\�����ł́A���z�d���̌����ɂ��A�ލ������������ւ��邱�Ƃ��ł���B
|